Draft:Discrete Paired Transforms

“Keyword” content=”fast Fourier transform, paired transform, paired transformation, paired representation, paired functions, splitting-signals, paired FFT, fast paired transform, fast paired Fourier transform, paired transform-based DFT, paired transform-based FFT, time- frequency analysis, frequency-time representation, integer Fourier transform.”

I. Introduction

The unitary 1-D discrete paired transformation (DPT) was introduced by Grigoryan and published n in 1986 [1].This transformation has been extracted from the discrete Fourier transform (DFT), namely the paired transform reveals the mathematical structure of the DFT.The complete set of paired functions are frequency-time type wavelets [2]-[4]. The system of paired functions is numbered by two parameters, namely, one parameter for the frequency and one parameter for the time. The N-point discrete paired transformation first was developed for orders N which are powers of two, $N=2^{r}$, r ≥ 1 . This transform splits the N-point DFT into N/2, N/4, N/8, ..., 2, 1, and 1-point DFT, and the signal is represented by (r + 1) short signals of lengths N/2, N/4, N/8, ..., 2, 1, and 1-point. In the general case when $N=L^{r}$ , where L ≥ 2 and r > 1, and for the case when N is a composite integer, the DPT is also defined [4].

II. Paired representation of the signal

The paired transformation of the signal is the 2-D frequency plus 1-D time representation of the signal. The signal {fn} of length $N=2^{r}$,r > 2, is transfromed into a set of splitting-signals {fp',pt; t = 0∶ N/(2p)-1},$p=2^{k}$,k = 0∶ r. This is a frequency (p) and time (t) representation of the signal, which is accomplished by the fast paired transform [2]-[8]. The splitting-signals carry the information of the Fourier transform of the original signal ${f_{n}}$ in disjoint subsets of frequency-points. The splitting of the signal is performed by the N-point discrete paired transformation χ'N whose basis functions χ'p,t(n) are defined by

File:Screen Shot 2014-11-30 at 2.28.59 PM.png

if p > 0, and χ^' 0,0(n) ≡ 1. The complete system of paired functions is composed as

File:Screen Shot 2014-11-30 at 2.50.54 PM.png

which defines the unitary paired transformation χ′. The double numbering of the paired func- tions χ'p,pt(n) refers to the frequency-point (p = 2k) and time (pt) which runs the interval of time points {0, 1, 2, ..., N/2 − 1} with the step (“velocity”) equals p. The change in time deter- mines the series of functions, and the total number of pairs numbering the system of functions, if such is complete, has to be equal to N.

The basic paired functions can also be defined by extreme and zero values of certain cosine waves, when they run through the interval [0,N −1] with different frequencies ωk = (2π/N)2k, where k = 0∶ (r - 1). Indeed, we can write that

File:Screen Shot 2014-11-30 at 3.23.13 PM.png

where t = 0∶ (2r-k-1 - 1),k = 0∶ (r - 1), and Q[x] denotes the following quantization function of the interval [−1, 1] : Q[x] = x, if |x| = 1, and Q[x] = 0, otherwise. As an example, Figure 1 illustrates the process of composition of these functions from the corresponding cosine waves defined in the interval [0, 7]. The first series consists of four shifted

File:Screen Shot 2014-12-11 at 9.39.13 PM.png

Fig. 1. (a) Cosine waves and (b) discrete paired functions for N = 8.

versions of the cosine functions with frequency ω0 = π/4. The next series consists of two shifted versions of the cosine function with frequency 2ω0. There are also one cosine function with frequency 4ω0 and one constant function. Extremum values of all these eight waves define exactly the matrix of the 8-point discrete paired transformation.

A. Matrix of the paired transform

The matrix of the eight-point discrete paired transform (DPT) is defined as

File:Screen Shot 2014-12-07 at 7.55.07 PM.png

The normalized coefficients {√2,√2,√2,√2,2,2,2√2,2√2} of rows can be considered, to make this transform unitary. The first four basis paired functions correspond to the frequency p = 1, the next two functions correspond to frequency p = 2, and the last two functions correspond to the frequencies p = 4 and 0, respectively. In the general N = 2rcase, the system of complete paired functions is generated sequentially from the systems of small orders N/2, N/4, ... in the following way:

File:Screen Shot 2014-12-01 at 9.20.58 PM.png

where $I_{M}$ denotes the identity matrix (M×M). For instance, for $N=16$,

File:Screen Shot 2014-12-01 at 9.30.34 PM.png

B. splitting-signale

The components of the splitting-signal

File:Screen Shot 2014-12-01 at 9.36.15 PM.png

of the signal $f_{n}$ are calculated by

File:Screen Shot 2014-12-02 at 4.49.18 PM.png

The last one-point splitting-signal is

File:Screen Shot 2014-12-02 at 5.02.15 PM.png

In paired representation, the signal $f_{n}$ is transformed into the following set of splitting-signals:

File:Screen Shot 2014-12-02 at 5.24.45 PM.png

For example, let $f_{n}$ be the signal {${1,2,2,4,5,3,1,3}$}. The paired transform of this signal results in the following four splitting-signals:

File:Screen Shot 2014-12-02 at 5.32.58 PM.png

C. DFT and splitting-signals

Splitting-signals carry the spectral information of the signal $f_{n}$ in different and disjoint subsets of frequency-points. In paired representation, the splitting of the N-point DFT

File:Screen Shot 2014-12-02 at 5.39.01 PM.png

by $(r+1)$ short DFTs is based on the following formula [1], [3]:

File:Screen Shot 2014-12-02 at 6.09.58 PM.png

For the set of frequency-points {$p=2^{k}$; k = 0 : (r − 1)}, the disjoint subsets

File:Screen Shot 2014-12-02 at 6.14.57 PM.png

together with $T_{0}^{'}$ = {0} divide the set of N frequency-points $X_{N}$ = {0, 1, 2, ..., N−1}. Therefore, the splitting-signal generated by the frequency $p=2^{n}$ is denoted by

File:Screen Shot 2014-12-02 at 6.20.42 PM.png

C.1 The first splitting-signal

To describe the meaning of equation (4), we first consider the p = 1 case, when the first splitting-signal carries the spectral information of the signal at all odd frequency-points,

File:Screen Shot 2014-12-02 at 6.27.31 PM.png

The N/2-point DFT over the modified splitting-signal

File:Screen Shot 2014-12-02 at 6.35.18 PM.png

equals the N-point DFT of the original signal at odd frequency-points.

C.2 The second splitting-signal

For the $p=2$ case, the splitting-signal is

File:Screen Shot 2014-12-02 at 6.43.51 PM.png

and

File:Screen Shot 2014-12-02 at 7.02.29 PM.png

The N/4-point DFT over the modified splitting-signal

File:Screen Shot 2014-12-02 at 7.09.47 PM.png

equals the N-point DFT of the original signal at all frequency-points which are odd-integer multiple of 2.

Example 1: Consider the signal fn of length N = 256, which is shown in Figure 2 in part a. The paired transform of the signal, as the set of splitting-signals {f_(T_1^' ),f_(T_2^' ),f_(T_4^' ),f_(T_8^' )…,f_(T_128^' ),f_(T_0^' ) } is shown in part b. The vertical dashed lines separate the first seven splitting-signals.
Figure 3 shows the 256-point DFT of the signal in absolute mode in part a. In part b, the same DFT is shown, but in the order that corresponds to the partition of the frequency- points {0,1,2,...,255} by subsetsT1',T2',T4',...,T1'28, and T0′. The first part with 128 values corresponds to the 128-point DFT of the modified splitting-signal f1′,tWt, which is also the 128-point SDFT of the splitting-signal f1′,t. The next part with 64 values corresponds to the 64-point DFT of the modified splitting-signal f2′,2tW1t28, which is also the 64-point SDFT of the splitting-signal f2′,2t, and so on.

File:Screen Shot 2014-12-11 at 9.55.23 PM.png

Fig. 2. (a) The signal of length 256 and (b) the 256-point discrete paired transform.

File:Screen Shot 2014-12-11 at 9.34.54 PM.png

Fig. 3. (a) DFT of the signal and (b) DFTs of the modified splitting-signals. (The transforms are shown in absolute mode.)

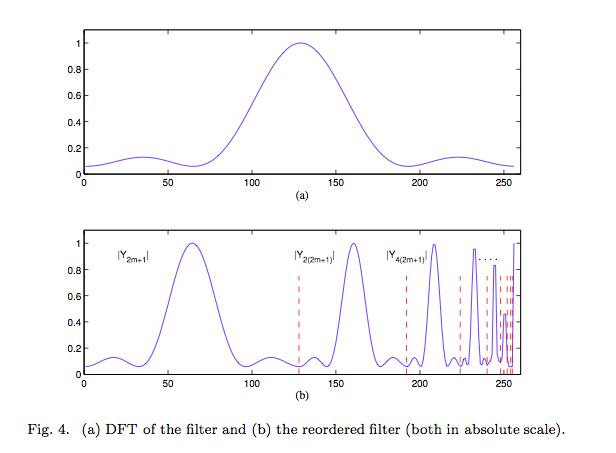
Example 2: We consider the smoothing of the signal by the circular convolution with the impulse response

File:Screen Shot 2014-12-06 at 5.18.07 PM.png

with value $y_{n}=5$. Figure 4 shows the frequency characteristics $Y_{p}$ of $y_{n}$ in absolute mode in part a. In part b, this characteristics is shown in the same order as $F_{p}$ in part b of Figure 3. These characteristics are used to filter the corresponding modified splitting-signals and they are separated in the graph by vertical lines.

(a) DFT of the filter and (b) the reordered filter (both in absolute scale).

III. Paired transform-based fast Fourier transform

A. Fast 8-point DFT

N = 4 case. The set X ={0,1,2,3} is covered by the partition σ^'=(T_1^',T_2^',T_0^' ) with subsets T1' = {1,3},T2' = {2},and T0' = {0}. For the generators p = 1,2, and 0 of the subsets Tp′, the following matrix (4 × 3) with values of t = (np) mod 4, when n = 0 : 3, is composed:

File:Screen Shot 2014-12-06 at 5.40.56 PM.png

A length-4 sequence $f_{n}$ can thus be represented as three short sequences

File:Screen Shot 2014-12-06 at 5.26.24 PM.png

This representation is performed by the paired transformation $X_{4}^{'}$ with the matrix

File:Screen Shot 2014-12-06 at 5.40.45 PM.png

The decomposition of the 4-point DFT by the paired transform into the 2- and 1-point DFTs can be written in matrix form as

File:Screen Shot 2014-12-06 at 5.40.24 PM.png

B. Fast 8-point DFT

Let fn be a sequence (signal) of length 8. The set X = {0, 1, ..., 7} is covered by the following partition of subsets σ^'=(T_1^',T_2^',T_4^',T_0^' ),where subsets T1′ ={1,3,5,7},T2′ ={2,6},T4′ ={4} and T0′ = {0}. The partition of X by subsets T_p^' is unique. For the generators of these subsets

File:Screen Shot 2014-12-07 at 3.03.02 PM.png

Elements of this matrix show a way of calculating the matrix of the eight-point discrete paired transform. Indeed, it follows from this matrix that the signal $f_{n}$ is represented in paired form as the following four splitting-signals:

File:Screen Shot 2014-12-07 at 3.12.35 PM.png

All components of these four signals are calculated by the paired transformation $X_{8}^{'}$ with the matrix

File:Screen Shot 2014-12-07 at 3.26.25 PM.png

Each splitting-signal carries the spectral information at frequency-points of the corresponding subset $T_{p}^{'}$ . Thus , for $p=1$

File:Screen Shot 2014-12-07 at 3.36.40 PM.png

for $p=2$

File:Screen Shot 2014-12-07 at 3.40.10 PM.png

and for p = 4 and 0, we obtain respectively f4',0 = F4 and f0^',0 = F0.
 The decomposition of the 8-point DFT by the paired transform can thus be written in matrix form as

File:Screen Shot 2014-12-16 at 6.32.40 PM.png

where D8 is the diagonal matrix with coefficients {1,W 1,-j,W 3,1,-j,1,1} and W = exp(-jπ/4). The signal-flow graph for calculation of the eight-point DFT by the paired transforms is shown in Fig. 5 and its block-diagram in Fig. 6. The matrix of the 2-point paired transformation equals [χ'2]=[1-1,1 1].We now consider the signal-flow graph of Fig. 6 for the case when the input sequence fn is real. There are two operation√s of multiplication by non-trivial complex factors W = (1-j)a and W 3 = (-1 - j)a,where a = 2/2, to be used over the output of the 8-point paired transform. Three trivial multiplications by −j are also used in calculation. All inputs and outputs of the paired transforms χ'8,χ'4, and χ′2 as well as multiplications by complex factors can be split into two parts as shown in Fig. 7. The new signal-flow graph can then be simplified. One can see that calculations for real Rp and imaginary Ip parts of transform coefficients Fp have been separated in a symmetric way. This figure shows also values of all inputs and outputs for each transform in the block-scheme, when the sequence {fn} equals {1, 2, 4, 4, 3, 7, 5, 8}.

File:Screen Shot 2014-12-11 at 9.16.27 PM.png

Fig. 5. The signal-flow graph for computing the eight-point DFT.

File:Screen Shot 2014-12-11 at 9.30.35 PM.png

Fig. 6. Block-scheme of calculation of the 8-point DFT by paired transforms.

C. 16-point paired FFT

The simplified signal-flow graph for calculating the 16-point DFT is shown in Fig. 8. The following relations between Fourier coefficients for a real input, R16-p =Rp,I16-p =-Ip,when p=1:7. The calculation of the 16-point DFT by the simplified signal-flow graph requires m′(16) = 12 real multiplications by factors a = cos(π/4), b = cos(π/8), and c = cos(3π/8). We denote by χ'8;in two incomplete 8-point paired transforms with one zero input and for which only the last four outputs are calculated. These transforms over an input x = (x0 , x1, ..., x7)′ are described

File:Screen Shot 2014-12-11 at 9.23.58 PM.png

Fig. 7. Block-scheme of calculation of real and imaginary parts of the 8-point DFT.

File:Screen Shot 2014-12-11 at 9.27.17 PM.png

Fig. 8. Block-scheme of calculation of the 16-point DFT of a real input fn, n = 0 : 15.

in matrix form as

File:Screen Shot 2014-12-07 at 8.57.47 PM.png

and

File:Screen Shot 2014-12-07 at 8.54.24 PM.png

Two incomplete 8-point paired transforms require 9 additions each. Two incomplete 4-point paired transforms χ'4;in are used for calculation of the last two outputs. The incomplete 4-point paired transforms require 3 additions each. The total number of the required additions is thus calculated as

File:Screen Shot 2014-12-07 at 8.51.58 PM.png

The proposed calculation of the N-point DFT by the simplified flow graph can be used for real and imaginary inputs separately. Therefore the number of operations of multiplication is counted as twice those estimates derived for real inputs. The number of additions is counted as twice those estimates derived for real inputs, plus extra additions are needed to combine the first (N − 2) DFT outputs produced from real and imaginary inputs. For instance, for the 16-point DFT of complex data, the number of additions equals $2(58)+2(14)=144$. For the 8-point DFT of complex data, the number of additions equals $2(20)+2(6)=52$. The same estimates were also reported in [10], [11].

References

[1] A.M. Grigoryan, “New algorithms for computing discrete Fourier transforms,” Journal of Computation Mathematics and Mathematical Phisics, AS USSR, vol. 26, no. 9, pp. 1407–1412, Moscow 1986 (available in http://www.fasttransforms.com/?b=1&l=6)

[2] A.M. Grigoryan, and S.S. Agaian, “Split manageable efficient algorithm for Fourier and Hadamard trans- forms,” IEEE Trans. on Signal Processing, vol. 48, no. 1, pp. 172-183, Jan. 2000.

[3] A. M. Grigoryan, “2-D and 1-D Multipaired transforms: frequency-time type wavelets,” Signal Processing, IEEE Transactions on, vol. 49, no. 2, pp. 344–353, 2001.

[4] A.M. Grigoryan and S.S. Agaian, Multidimensional Discrete Unitary Transforms: Representation, Par- titioning, and Algorithms, New York: Marcel Dekker, 2003.

[5] J. U. Anugom and A. M. Grigoryan, “Method of splitting signals by the paired transform,” in Industrial Electronics, 2006 IEEE International Symposium on, vol. 1, pp. 548–552, 2006.

[6] F.T. Arslan, A.K. Chan, and A.M. Grigoryan, “Directional denoising of aerial images by splitting-signals,” in Region 5 Conference, 2006 IEEE, pp. 114–119, 2006.

[7] A. M. Grigoryan, “Representation of the Fourier transform by Fourier series,” in Journal Mathematical Imaging and Vision, vol. 25, pp. 87–105, 2006.

[8] P. Patel, N. Ranganath, and A.M. Grigoryan, “Performances of Texas Instruments DSP and Xilinx FPGAS for Cooley-Tukey and Grigoryan FFT algorithms,” The Journal of Engineering Technology, vol. 1, p. 83, 2011.

[9] A.M. Grigoryan and M.M. Grigoryan, Brief Notes in Advanced DSP: Fourier Analysis With MATLAB., CRC Press Taylor and Francis Group, 2009.

[10] P. Duhamel, “Implementation of “Split-radix” FFT algorithms for complex, real, and real-symmetric data,” IEEE Trans. ASSP-34, no. 2, pp. 285 - 295, 1986.

[11] G. Bi and Y. Zeng, Transforms and Fast Algorithms for Signal Analysis and and Representations, Birkhauser Verlag, Oct. 2003.