Distribution (Mathematik)
Eine Distribution im Bereich der Mathematik bezeichnet ein Objekt aus der Funktionalanalysis, das je nach Blickwinkel als eine Verallgemeinerung des Begriffs der Funktion angesehen wird. Mathematisch präzise handelt es sich allerdings nur um eine besondere Art eines Funktionals.
Die Theorie der Distributionen ermöglicht es, Funktionen abzuleiten, die im klassischen Sinn nicht differenzierbar sind. Aus diesem Grund eignen sich die Distributionen besonders für das Lösen partieller Differentialgleichungen. So existieren partielle Differentialgleichungen, die keine klassische Lösung haben, jedoch Lösungen im distributionellen Sinn besitzen. Die Theorie der Distributionen ist auch in der Physik und in den Ingenieurwissenschaften wichtig. Viele der dort untersuchten Probleme führen nämlich zu Differentialgleichungen, die mit Hilfe der Theorie der Distributionen gelöst werden konnten.
Der Mathematiker Laurent Schwartz war maßgeblich an der Untersuchung der Theorie der Distributionen beteiligt. Im Jahr 1950 veröffentlichte er den ersten systematischen Zugang zu dieser Theorie. Für seine Arbeiten über die Distributionen erhielt er die Fields-Medaille.
Geschichte der Distributionentheorie
Schon im Jahr 1903 führte Jacques Hadamard den für die Distributionentheorie wichtigen Begriff des Funktionals ein. Aus heutiger Sicht ist ein Funktional eine Funktion, die anderen Funktionen eine Zahl zuordnet. Insbesondere konnte Hadamard zeigen, dass jedes stetige, lineare Funktional als Grenzwert einer Folge von Integralen

geschrieben werden kann. Hierbei dürfen Grenzwert und Integral im Allgemeinen nicht vertauscht werden. Im Jahr 1910 konnte gezeigt werden, dass jedes stetige, lineare Funktional auf , dem Raum der p-integierbaren Funktionen, als
mit und dargestellt werden kann. Hier muss also kein Grenzwert gebildet werden und ist eindeutig bestimmt. Deshalb wird das Funktional oftmals mit der "Funktion" identifiziert; hat hier also zwei Bedeutungen: Zum einen versteht man als -"Funktion", zum anderen wird es mit dem Funktional gleichgesetzt.

Als erster beschäftigte sich Paul Dirac in den 1920er-Jahren bei Forschungen in der Quantenmechanik mit Distributionen.[1] Insbesondere die Delta-Distribution geht auf sein Werk zurück. Jedoch kannte er noch keine mathematisch präzise Definition für das Objekt. Auch ließ er bei seinen Untersuchungen die damalige Funktionalanalysis, also die Theorie der Funktionale, außer Acht. In den 1930er-Jahren beschäftigte sich Sergei Lwowitsch Sobolew mit Anfangswertproblemen bei partiellen hyperbolischen Differentialgleichungen. Bei diesen Untersuchungen führte er die heute nach ihm benannten Sobolew-Räume ein. Im Jahr 1936 untersuchte Sobolew eine hyperbolische Differentialgleichung zweiter Ordnung mit analytischen Koeffizientenfunktionen; um ein griffigeres Kriterium für die Existenz einer Lösung dieser partiellen Differentialgleichung angeben zu können, erweiterte Sobolew die Fragestellung auf den Raum der Funktionale.[2] Damit war er der erste, der die heutige Definition einer Distribution formulierte. Jedoch entwickelte Sobolew keine umfassende Theorie aus seinen Definitionen, er verwendete sie nur als Hilfsmittel im Zusammenhang mit partiellen Differentialgleichungen.

Schließlich entwickelte Laurent Schwartz die Theorie der Distributionen im Winter 1944/45. Zu diesem Zeitpunkt waren ihm Sobolews Arbeiten noch unbekannt; doch auch er stieß genau wie Sobolew durch Fragen im Bereich der partiellen Differentialgleichungen auf spezielle Funktionale, die er nun Distributionen nannte.[3] Von da an wurde die Theorie derart schnell weiterentwickelt, dass Schwartz darüber schon im Winter 1945/46 Vorlesungen in Paris halten konnte. Elektrotechniker, die seine Vorlesungen besuchten, drängten ihn dazu, seine Theorie in Richtung der Fourier- und der Laplacetransformationen weiterzuentwickeln. Im Jahr 1947 hatte Schwartz den Raum der temperierten Distributionen definiert und somit die Fourier-Transformationen in seine Theorie integriert. 1950/51 erschien seine Monographie Theorie des Distributions, wodurch seine Theorie weiter gefestigt wurde. Schon 1950 erhielt er für seine Forschungen im Bereich der Distributionen die Fields-Medaille, eine der höchsten Auszeichnungen im Bereich der Mathematik.
Die Theorie der Distributionen wurde von dort an in der theoretischen Physik und in der Theorie der partiellen Differentialgleichungen weiterentwickelt. Die Distributionentheorie ist nützlich, um singuläre Objekte der Physik wie zum Beispiel die elektromagnetische Punktladung oder die Punktmasse mathematisch präzise zu beschreiben. Diese beiden physikalischen Objekte können mit Hilfe der Delta-Distribution geeignet beschrieben werden; denn von der räumlichen Dichtefunktion eines Massenpunktes mit Einheitsmasse wird gefordert, dass sie überall verschwindet, außer an einem Punkt. Dort muss sie unendlich werden, da das Raumintegral über die Dichtefunktion 1 ergeben soll (Einheitsmasse). Es gibt keine Funktion, die diese Eigenschaften erfüllt. In der Theorie der partiellen Differentialgleichungen und der Fourieranalyse sind Distributionen wichtig, da mit dieser Begriffsbildung jeder L2-Funktion eine Ableitung zugeordnet werden kann.
Testfunktionen
Eine Distribution ist ein stetiges und lineares Funktional auf dem Raum der Testfunktionen. Zum besseren Verständnis wird hier kurz dargelegt, was eine Testfunktion ist. Insbesondere muss der Raum der Testfunktionen eine Topologie tragen, damit der Begriff der Stetigkeit überhaupt Sinn ergibt. Diese Topologie wird auf dem Raum durch einen Konvergenzbegriff festgelegt. Erst im nächsten Abschnitt wird näher auf die Definition einer Distribution eingegangen.
Es bezeichnet
die Menge aller unendlich oft differenzierbaren Funktionen, die einen kompakten Träger haben, also außerhalb einer kompakten Menge gleich null sind. Der Konvergenzbegriff wird nun festgelegt, indem man sagt: Eine Folge mit konvergiert gegen , wenn es ein Kompaktum gibt mit für alle und
für alle Multiindizes . Die Menge ist – ausgestattet mit diesem Konvergenzbegriff – ein lokalkonvexer Raum, den man Raum der Testfunktionen nennt und mit bezeichnet.
Definition
Eine Distribution ist eine stetige und lineare Funktion von einem Testfunktionenraum in die reellen Zahlen oder komplexen Zahlen. Solche Funktionen werden traditionell als Funktionale bezeichnet.
Die Menge der Distributionen mit den entsprechenden Verknüpfungen der Addition und der Skalarmultiplikation ist also der topologische Dualraum zum Testfunktionenraum und wird hier mit einem gekennzeichnet. So ist zum Beispiel der topologische Dualraum zu . Da die Teilmengenrelation gilt, beschränkt der Artikel sich soweit möglich auf den Raum . Da bei linearen Funktionalen die Eigenschaften Beschränktheit und Stetigkeit äquivalent sind, findet man in der Literatur auch die Definition:
Eine lineare Funktion heißt Distribution, wenn es für jedes Kompaktum , für alle Konstanten und mit
gibt. Wenn für alle Kompakta dieselbe Zahl gewählt werden kann, so wird diese als Ordnung von bezeichnet.
Zwei unterschiedliche Sichtweisen
Im Abschnitt zur Definition der Distribution wurde gesagt, dass eine Distribution ein Funktional, also insbesondere eine Funktion ist. Jedoch wurde im Abschnitt Geschichte der Distributionentheorie schon gesagt, dass die Delta-Distribution keine Funktion sein kann. Dies ist offensichtlich ein Widerspruch, welcher sich auch noch in der aktuellen Literatur wiederfindet. Dieser Widerspruch entsteht dadurch, dass man auch bei Distributionen, genauso wie bei Funktionalen auf -Räumen, versucht das Funktional mit einer reellenwertigen Funktion zu identifizieren.
Insbesondere in der theoretischen Physik versteht man unter einer Distribution ein Objekt mit gewissen sich aus dem Kontext ergebenden Eigenschaften. Die gewünschten Eigenschaften verhindern oftmals, dass eine Funktion sein kann, aus diesem Grund spricht man dann von einer verallgemeinerten Funktion. Nachdem nun die Eigenschaften von festgelegt sind, betrachtet man die Zuordnung
die einer Testfunktion eine reelle Zahl zuordnet. Da jedoch im Allgemeinen keine Funktion ist, muss für den Ausdruck von Fall zu Fall erst ein Sinn erklärt werden.
Mathematisch gesehen ist eine Distribution eine Funktion mit bestimmten abstrakten Eigenschaften (Linearität und Stetigkeit), die einer Testfunktion eine reelle Zahl zuordnet. Ist das aus vorigem Abschnitt eine integrierbare Funktion, so ist der Ausdruck mathematisch präzise definiert. Jedoch wird hier nicht die Funktion als Distribution bezeichnet, sondern das Funktional heißt Distribution.
Allerdings unterscheiden auch viele Mathematikbücher nicht zwischen der (distributions)erzeugenden Funktion und der Distribution an sich. In diesem Artikel wird vorwiegend die mathematische Sichtweise verwendet.
Beispiele
- Sei und , so ist durch für alle eine Distribution definiert.
- Sei und . Dann ist für alle die partielle Ableitung ebenfalls eine Distribution aus .
- Der Cauchy'sche Hauptwert der Funktion kann ebenfalls als Distribution aufgefasst werden. Man setzt
- .
Delta-Distribution
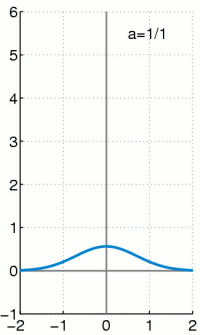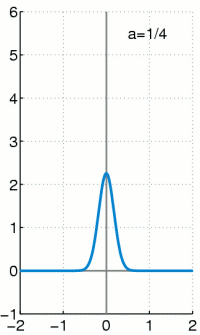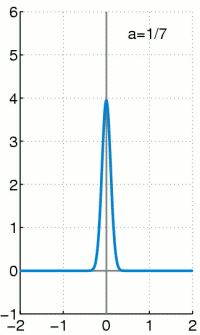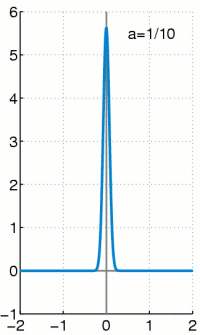
Die Delta-Distribution ist eine irreguläre Distribution. Das heißt sie kann nicht durch eine gewöhnliche Funktion dargestellt werden, obwohl sie oft wie eine solche geschrieben wird. Es gilt:
Sprich: Die Delta-Distribution angewendet auf eine Testfunktion ergibt die Testfunktion ausgewertet an der Stelle 0.
Dies ist ein Spezialfall der folgenden allgemeineren Definition mit :
Die Schreibweise „wie eine gewöhnliche Funktion“ ist .
Radon-Maße
Mit wird die Menge aller Radon-Maße bezeichnet. Sei Nun kann man mittels
jedem eine Distribution zuordnen. Auf diese Weise kann man stetig in einbetten.
Poisson-Gleichung
Ein prominentes Beispiel ist die formale Identität
aus der Elektrostatik, die im Zusammenhang mit dem Integral
auftritt. Man kann die oben angegebene Identität benutzen, um nachzuweisen, dass U die Poisson-Gleichung
löst. ist der Laplace-Operator. Bei Verwendung von Distributionen, d.h. bei Differentiation unter dem Integral, erhält man mit den Eigenschaften der unten ausführlich behandelten Delta-Distribution sehr schnell eine sog. „schwache Lösung“, die dann gegebenenfalls noch „regularisiert“ werden kann (z. B.: wenn stetig ist, ist zweimal stetig differenzierbar und erfüllt die Poisson-Gleichung im gewöhnlichen Sinn).
Oszillierendes Integral
Für alle Symbole wird durch das oszillierende Integral
eine Distribution erzeugt. Diese Distribution wird zu meist durch die Integraldarstellung
beschrieben. Oszillierende Integrale konvergieren im Allgemeinen jedoch nicht im lebesguesinn, daher können das oszillierende Integral und das außenstehende Lebesgue-Integral nicht vertauscht werden.
Konvergenz
Da Distributionenräume als topologische Dualräume definiert wurden, erhält man auf den Dualräumen sofort eine Topologie. Dies ist im Fall der Distributionenräume die Schwach-*-Topologie. Daher ist der Distributionenraum mit einem Konvergenzbegriff ausgestattet. Eine Folge von Distributionen konvergiert gegen , wenn
für jedes gilt.
Da man ein mit identifizieren kann, kann man als einen Teilraum von auffassen.
Insbesondere liegt der Raum dicht in . Das bedeutet also, dass für ein eine Folge in mit in existiert. Man kann also jede Distribution durch
darstellen.
Regularität und singulärer Träger
Reguläre Distributionen
Reguläre Distributionen lassen sich als Integraloperatoren schreiben. Es gibt also eine Darstellung
mit eine lokal integrierbare Funktion. Nicht alle Distributionen lassen sich auf diese Weise schreiben, weil es nicht immer eine solche Funktion gibt. Würde man zum Beispiel die Delta-Distribution als reguläre Distribution annehmen, erhält man den Widerspruch (als Distribution).
In der Praxis verwendet man jedoch diese Schreibweise auch für nicht reguläre Distributionen. Jedoch muss einem dabei bewusst sein, dass dies nur eine Schreibweise ist.
Träger
Sei eine Distribution. Man sagt, dass ein Punkt zum Träger von gehört und, schreibt , wenn für jede offene Umgebung von eine Funktion existiert mit .
Falls eine reguläre Distribution ist, so ist diese Definition äquivalent zur Definition des Trägers einer Funktion.
Kompakter Träger
Eine Distribution hat einen kompakten Träger, wenn ein kompakter Raum ist. Die Menge der Distributionen mit kompaktem Träger wird mit bezeichnet. Dieser Raum ist ein Untervektorraum von und der topologische Dualraum zu . Wobei der Raum der glatten Funktionen mit einer abzählbaren Familie von Halbnormen
die eine lokalkonvexe Topologie erzeugt.
Singulärer Träger
Sei eine Distribution. Man sagt, dass ein Punkt nicht zum singulären Träger gehört, wenn es eine offene Umgebung von und eine Funktion gibt mit
für alle .
Es gilt also genau dann, wenn es keine offene Umgebung von gibt, sodass die Einschränkung von auf gleich einer glatten Funktion ist. Insbesondere ist der singuläre Träger einer nicht regulären Distribution nicht leer.
Operationen auf Distributionen
Da die drei zu Anfang behandelten Distributionenräume Vektorräume sind, sind die Addition von Distributionen und die Multiplikation einer komplexen Zahl mit einer Distribution schon definiert. Im Folgenden werden noch die Multiplikation einer Funktion mit einer Distribution die Ableitung einer Distribution und die Faltung einer Distribution mit einer glatten Funktion definiert.
Multiplikation mit einer Funktion
Sei und . Dann wird die Distribution definiert als
- .
Differentiation
Motivation
Betrachtet man eine stetig differenzierbare Funktion und die ihr zugeordnete reguläre Distribution , so erhält man die Rechenregel
Hierbei wurde partielle Integration verwendet, wobei die Randterme wegen der gewählten Eigenschaften der Testfunktion wegfallen. Dies entspricht der schwachen Ableitung. Die äußeren beiden Terme sind auch für singuläre Distributionen definiert, und man verwendet dies zur Definition der Ableitung einer beliebigen Distribution .
Definition
Sei also eine Distribution und ein Multiindex. Dann wird eine Distribution definiert als
- .
Beispiel
Die Heaviside-Funktion ist durch
definiert. Sie ist mit Ausnahme von überall differenzierbar. Man kann sie als reguläre Distribution betrachten, und die Rechnung
zeigt, dass ihre Ableitung (als Distribution) die Delta-Distribution ist:
Man kann außerdem die Delta-Distribution selbst noch ableiten:
Die Ableitungen der Delta-Distribution sind also ( bis auf den zusätzlichen Vorzeichenfaktor ) gleich den Ableitungen der Testfunktion an der Stelle
Tensorprodukt
Motivation
Sei die Menge als Produktraum mit gegeben. Dann kann auf den Funktionen und mittels der Vorschrift
ein Tensorprodukt definieren. Analog dazu kann man ein Tensorprodukt zwischen Distributionen definieren. Dazu kann man zuerst reguläre Distributionen betrachten. Seien und zwei lokal-integrierbare Funktionen, so folgt aus obiger Definition
für alle Daraus folgt
Hieraus leitet man folgende Definition ab.
Definition
Seien und . Dann ist eine Distribution aus , welche durch
definiert ist.
Faltung mit einer Funktion
Definition
Sei eine Distribution und eine Funktion so ist die Faltung definiert durch
- .
Eigenschaften
- Falls eine glatte Funktion ist, so stimmt die Definition mit der Faltung von Funktionen überein.
- Das Ergebnis der Faltung ist eine glatte Funktion, also gilt
- .
- Für und ist die Faltung assoziativ, also gilt
- .
- Für jeden Multi-Index gilt für die Ableitung der Faltung
- .
Faltung zweier Distributionen
Existenz- und Eindeutigkeitsaussage
Sei eine lineare Abbildung von nach , welche stetig ist, was in für in bedeutet. Außerdem kommutiert mit allen Translationen , was meint. Dann existiert eine eindeutige Distribution , so dass
für alle gilt.
Definition
Seien und zwei Distributionen, wobei eine kompakten Träger hat. Dann ist für alle die Faltung zwischen diesen Distributionen definiert durch
- .
Die Abbildung
ist linear, translationsinvariant und stetig. Daher gibt es auf Grund obigen Satzes eine eindeutige Distribution , so dass
für alle gilt.
Eigenschaften
Diese Definition ist eine Verallgemeinerung der hier schon erwähnten Definitionen. Wählt man für eine reguläre Distribution, also eine Funktion, so entspricht dies den hier aufgeführten Definitionen. Es gelten die Eigenschaften:
- Die Faltung ist kommutativ
- Für den Träger gilt
- ,
- und für den singulären Träger erhält man
- .
Fourier-Transformation
Um eine Kontinuierliche Fourier-Transformation auf Distributionen definieren zu können, muss man die Menge der Distributionen erst einmal einschränken. Genauso wie nicht jede Funktion fouriertransformierbar ist, kann man auch nicht für jede Distribution die Fouriertransformation erklären. Aus diesem Grund entwickelte Laurent Schwartz den heute nach ihm benannten Schwartz-Raum . Auf diesem Raum ist die Fourier-Transformation ein Automorphismus. Sein topologischen Dualraum, also der Raum der stetigen, linearen Funktionale von , ist eine Teilmenge von und heißt Raum der temperierten Distributionen. Dieser Dualraum wird mit notiert und die Fouriertransformation von kann für alle durch
definiert werden. Auch auf diesem Raum ist die Fouriertransformation ein Automorphismus, also eine stetige, lineare und bijektive Abbildung auf .
Differentialgleichungen
Da jede - beziehungsweise sogar jede lokal-integrierbare -Funktion eine Distribution erzeugt, kann man diesen Funktionen im schwachen Sinn eine Distribution als Ableitung zuordnen. Lässt man Distributionen als Lösung einer Differentialgleichung so vergrößert sich der Lösungsraum dieser Gleichung natürlich. Im Folgenden wird kurz dargelegt, was eine distributionelle Lösung einer Differentialgleichung ist und wie die Fundamentallösung definiert ist.
Lösungen im Distributionensinne
Sei
ein Differentialoperator mit glatten Koeffizientenfunktionen . Eine Distribution heißt Distributionenlösung von , falls die von und erzeugten Distributionen übereinstimmen. Dies bedeutet
für alle . Falls die Distribution regulär und sogar m-mal stetig differenzierbar ist, dann ist ein klassische Lösung der Differentialgleichung.
Beispiel
Alle distributionellen Lösungen der eindimensionalen Differentialgleichung
sind die konstanten Funktionen. Das heißt, für alle wird die Gleichung
nur von konstanten gelöst.
Fundamentallösungen
Sei nun ein linearer Differentialoperator. Eine Distribution heißt Fundamentallösung, falls die Differentialgleichung
im Distributionensinne löst.
Die Menge aller Fundamentallösungen von ergibt sich durch Addition einer speziellen Fundamentallösung mit der allgemeinen homogenen Lösungen . Die allgemeine homogene Lösung ist die Menge der Distributionen für die gilt. Nach einem Satz von Bernard Malgrange besitzt jeder lineare Differentialoperator mit konstanten Koeffizienten eine Fundamentallösung .
Mit Hilfe dieser Fundamentallösungen erhält man durch Faltung Lösungen entsprechender inhomogener Differentialgleichungen. Sei eine glatte Funktion (oder allgemeiner eine Distribution mit kompaktem Träger), dann ergibt sich wegen
eine Lösung von in der Form
wobei genauso wie oben eine Fundamentallösung des Differentialoperators ist.
Harmonische Distributionen
Analog zu den harmonischen Funktionen definiert man auch harmonische Distributionen. So heißt eine Distribution harmonisch, wenn sie der Laplace-Gleichung
im distributionellen Sinne genügt. Da distributionelle Ableitung allgemeiner ist als das gewöhnliche Differential erwartet man auch mehr Lösungen der Laplace-Gleichung. Dies ist jedoch falsch. Denn man kann beweisen, dass es für jede harmonische Distribution eine glatte Funktion gibt, welche diese Distribution erzeugt. Es gibt also keine nicht-regulären Distributionen, welche die Gleichung erfüllen, insbesondere ist der singuläre Träger einer harmonischen Distribution leer. Diese Aussage gilt sogar allgemeiner für elliptische Differentialgleichungen.
Distributionen auf Mannigfaltigkeiten
Sei eine glatte Mannigfaltigkeit und sei ein System von Karten und sei , so dass
in für alle gilt. Man nennt das System eine Distribution in . Diese Distribution ist eindeutig bestimmt und von der Wahl der Karte unabhängig.
Es gibt noch andere Möglichkeiten Distributionen auf Mannigfaltigkeiten zu definieren. Dazu finden sich weitere Informationen im Artikel Dichtebündel. Die Definition dort hat den Vorteil, dass keine lokalen Karten gewählt werden müssen.
Einzelnachweise
- ↑ Paul Adrien Maurice Dirac: The principles of quantum mechanics, Clarendon Press, 1947
- ↑ Sergei Lwowitsch Sobolew: Méthode nouvelle à résoudre le problème de Cauchy pour les équations linéaires hyperboliques normales, Mat. Sb. 1, 1936, pp. 39–72
- ↑ Laurent Schwartz: Théorie des distributions 1–2, Hermann, 1950–1951
Literatur
- Lars Hörmander: The Analysis of Linear Partial Differential Operators I, Springer-Verlag, Second Edition, ISBN 3-540-52345-6
- Israel Gelfand: Verallgemeinerte Funktionen (Distributionen). Bände I - III (1958 mit G.E. Schilow), IV (1960 mit N.J. Wilenkin), V (1962 mit M.I. Graev und N.J. Wilenkin), VEB Deutscher Verlag der Wissenschaften, Berlin (Ost).
- Michael James Lighthill: An introduction to Fourier analysis and generalised functions, Cambridge University Press, Cambridge 2003, ISBN 0-521-09128-4.
- Joseph Wloka: Grundräume und Verallgemeinerte Funktionen, Lecture Notes in Mathematics 82, Springer-Verlag 1968, ISBN 3-540-04250-4.
- Bejancu, A.: Generalized function, in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, 2001, ISBN 978-1556080104
- Klaus-Heinrich Peters: Der Zusammenhang von Mathematik und Physik am Beispiel der Geschichte der Distributionen, Hamburg, 2004
























































































































































































