Datei:Discrete Hilbert transforms of a cosine function, using piecewise convolution.jpg
Seiteninhalte werden in anderen Sprachen nicht unterstützt.
Erscheinungsbild
Größe dieser Vorschau: 800 × 416 Pixel. Weitere Auflösungen: 320 × 166 Pixel | 640 × 333 Pixel | 1.108 × 576 Pixel
Originaldatei (1.108 × 576 Pixel, Dateigröße: 305 KB, MIME-Typ: image/jpeg)
![]()
Diese Datei und die Informationen unter dem roten Trennstrich werden aus dem zentralen Medienarchiv Wikimedia Commons eingebunden.
Beschreibung
| BeschreibungDiscrete Hilbert transforms of a cosine function, using piecewise convolution.jpg |
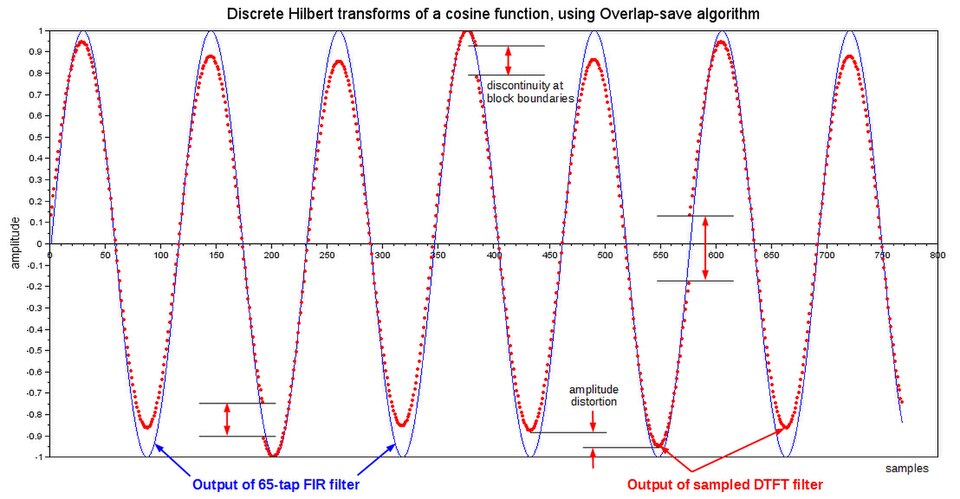
English: The blue graph shows a sine function that was created by computing the Discrete Hilbert transform of a cosine function. The cosine function was divided into 4 overlapping segments, which were individually convolved with an FIR Hilbert transform filter, and the 4 output segments were seamlessly pieced together. If the DFT of the FIR filter is replaced by the trivial samples of the DTFT of an IIR Hilbert transform filter, the cosine function segments are effectively convolved with a periodic summation of the IIR filter. That results in some frequency-dependent amplitude distortion and discontinuities at the segment boundaries. Examples of these effects are shown in the red graph. |
|||
| Datum | ||||
| Quelle | Eigenes Werk | |||
| Urheber | Bob K | |||
| Genehmigung (Weiternutzung dieser Datei) |
Ich, der Urheber dieses Werkes, veröffentliche es unter der folgenden Lizenz:
|
|||
| Andere Versionen |
Abgeleitete Werke dieser Datei: Discrete Hilbert transforms of a cosine function, using piecewise convolution.svg,
|
Scilab script
// Create a 64th-order Hilbert transform filter
M = 65;
h = hilb(M); // applies a rectangular window to the IIR function
// Derive overlap-save parameters
overlap = M-1;
N = 4*overlap; // an efficient block-size
step_size = N-overlap;
M2 = overlap/2; // length of the edge effects for a zero-phase (non-causal) filter
h = [h(1+M2:M) zeros(1,N-M) h(1:M2)]; // convert filter to zero-phase
H1 = fft(h, -1); // transfer function
H2 = %i*[0 -ones(1,N/2-1) ones(1,N/2)]; // or just sample the DTFT
// Create an input function
num_steps = 4; // signal length, in steps
n = (0 : num_steps*step_size+overlap)-M2; // sample indices (minus filter delay)
cycles_per_step = 5/3; // just a non-integer
cycles_per_sample = cycles_per_step / step_size;
x = cos(2*%pi*cycles_per_sample*n); // transform a pure sinusoid
// Overlap-Save convolution
position = 0;
while position+N <= length(x)
yt = real(fft(fft(x(position+(1:N)), -1) .* H1, 1));
y1(position+(1:step_size)) = yt(1+M2 : N-M2);
// The next 2 lines are equivalent, so the 2nd one is commented out.
yt = real(fft(fft(x(position+(1:N)), -1) .* H2, 1));
// yt = imag(hilbert(x(position+(1:N))));
y2(position+(1:step_size)) = yt(1+M2 : N-M2);
position = position + step_size;
end
// Compare the results
y1 = y1 / max(abs(y1));
y2 = y2 / max(abs(y2));
plot(y1, 'b');
plot(y2, 'r.');
title("Discrete Hilbert transforms of a cosine function, using Overlap-save algorithm", "fontsize", 4);
ylabel("amplitude", "fontsize", 3);
a = gca();
a.x_location = "origin";
a.children.children.mark_size=4; // size of red dots
Kurzbeschreibungen
Ergänze eine einzeilige Erklärung, was diese Datei darstellt.
Compare a simple FIR Hilbert transform filter to the IIR version provided by Matlab/Octave function hilbert().
In dieser Datei abgebildete Objekte
Motiv
Einige Werte ohne einen Wikidata-Eintrag
21. März 2015
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 17:34, 29. Mär. 2015 |  | 1.108 × 576 (305 KB) | Bob K | less gaudy |
| 01:03, 22. Mär. 2015 |  | 796 × 461 (283 KB) | Bob K | User created page with UploadWizard |
Dateiverwendung
Keine Seiten verwenden diese Datei.
Metadaten
Diese Datei enthält weitere Informationen (beispielsweise Exif-Metadaten), die in der Regel von der Digitalkamera oder dem verwendeten Scanner stammen. Durch nachträgliche Bearbeitung der Originaldatei können einige Details verändert worden sein.
| JPEG-Dateikommentar | Created with GIMP |
|---|


