Sinus und Kosinus

Graph der Sinusfunktion

Graph der Kosinusfunktion

Die Sinusfunktion und die Kosinusfunktion sind mathematische Funktionen aus der Klasse der trigonometrischen Funktionen. In einem rechtwinkligen Dreieck ist der Sinus eines Winkels das Verhältnis der Gegenkathete (das ist jene Kathete, die dem Winkel gegenüberliegt) zur Hypotenuse (also zur längsten Seite), der Kosinus ist das Verhältnis der Ankathete (das ist jene Kathete, die einen Schenkel des Winkel bildet) zur Hypotenuse.

Im rechtwinkeligen Dreieck lassen sich Sinus und Kosinus nur für Winkel zwischen 0 und 90 Grad definieren; für beliebige Winkel ist der Sinus als y-Koordinate und der Kosinus als x-Koordinate eines Punktes am Einheitskreis definiert, mittels Potenzreihendarstellung lässt sich die Definition auf komplexe Argumente verallgemeinern.

Geometrische Definition

Definition mit rechtwinkeligem Dreieck

Datei:RechtwinkligesDreieck.png

Dreieck mit einem rechten Winkel in C

Der Sinus und der Kosinus definieren sich über die Seitenverhältnisse im rechtwinkligen Dreieck. Betrachtet man den Winkel zwischen Hypotenuse und einer der beiden Katheten, dann ist der Sinus das Verhältnis von der dem Winkel gegenüberliegenden Seite (die eine Kathete ist) zur Hypotenuse, und der Kosinus das Verhältnis von der Kathete, die einen Schenkel des Winkel bildet, zur Hypotenuse (die den anderen Schenkel des Winkel bildet).

Formelmäßig gilt hier: Ist c die Hypotenuse und liegt der Winkel $\alpha$ zwischen c und der Kathete b, als der Kathete a gegenüber, dann ist der Sinus

\sin(\alpha )={\frac {a}{c}}

und der Kosinus

\cos(\alpha )={\frac {b}{c}}

Da aus geometrischen Gründen die Hypotenuse die längste Seite ist (denn sie liegt dem größten Winkel, also dem rechten Winkel, gegenüber), gelten auch stets $\sin(\alpha )\leq 1$ und $\cos(\alpha )\leq 1$ .

Betrachtet man statt $\alpha$ den gegenüberliegenden Winkel $\beta$ , so wechseln beide Katheten ihre Rolle, die Ankathete von $\alpha$ ist die Gegenkathete von $\beta$ und die Gegenkathete von $\alpha$ ist die Ankathete von $\beta$ , es gilt also

\sin(\beta )={\frac {b}{c}}

und

\cos(\beta )={\frac {a}{c}}

Da im rechtwinkeligen Dreieck $\alpha +\beta =90^{\circ }$ gilt, folgt

\cos(\alpha )=\sin(90^{\circ }-\alpha )

und

\sin(\alpha )=\cos(90^{\circ }-\alpha )

.

Auf dieser Beziehung beruht auch die Bezeichnung Kosinus, nämlich der Sinus des Komplementärwinkels.

Aus dem Satz des Pythagoras folgt die Beziehung

\sin ^{2}(\alpha )+\cos ^{2}(\alpha )=1\!

.

Definition mit Einheitskreis

Da im rechtwinkeligen Dreieck der Winkel zwischen Hypotenuse und Kathete zwischen 0 und 90 Grad ist, sind Sinus und Kosinus zunächst nur für solche Winkel definiert. Für eine allgemeine Definition betrachtet man einen Punkt $P$ mit den Koordinaten $(x,y)$ auf dem Einheitskreis, also $x^{2}+y^{2}=1$ . Der Ortsvektor von $P$ schließt mit der x-Achse einen Winkel $\alpha$ ein. Der Koordinatenursprung $(0,0)$ , der Punkt $(x,0)$ auf der x-Achse und der Punkt $P(x,y)$ bilden ein rechtwinkeliges Dreieck. Die Länge der Hyptonuse beträgt ${\sqrt {x^{2}+y^{2}}}=1$ . Die Ankathete des Winkels $\alpha$ ist der Vektor $(x,0)$ der Länge $x$ , es gilt also

\cos(\alpha )=x\!

,

die Gegenkathete des Winkels $\alpha$ ist der Vektor von $(x,0)$ nach $(x,y)$ , also der Vektor $(0,y)$ der Länge $y$ , es gilt also

\sin(\alpha )=y\!

.

Die y-Koordinate eines Punktes im ersten Quadranten des Einheitskreises entspricht also dem Sinus des Winkels zwischen seinem Ortsvektor und der x-Achse, die x-Koordinate dem Kosinus des Winkels. Setzt man diese Definiton in den anderen Quaddranten fort, so lassen sich Sinus und Kosinus für beliebige Winkel definieren.

Für negetaive Winkel betrachte man die Beziehung

\sin(-\alpha )=-\sin(\alpha )\!

und

\cos(-\alpha )=\cos(\alpha )\!

,

aus der sich Sinus und Cosinus für den vierten Quadranten, also Winkel zwischen -90 und 0 Grad berechnen lassen. Der Sinus ist also eine ungerade Funktion, der Kosinus eine gerade.

Für Winkel größer 90 Grad betrachte man die Beziehung

\sin(90^{\circ }+\alpha )=\sin(90^{\circ }-\alpha )

und

\cos(90^{\circ }+\alpha )=-\cos(90^{\circ }-\alpha )

,

aus der sich Sinus und Cosinus für den zweiten und dritten Quadranten, also Winkel zwischen 90 und 270 Grad berechnen lassen.

Für Winkel kleiner -90 Grad und größer 270 Grad ergeben sich Sinus und Kosinus aus den Beziehungen

\sin(\alpha )=\sin(\alpha +360^{\circ })

und

\cos(\alpha )=\cos(\alpha +360^{\circ })

;

Sinus und Kosinus sind also periodische Funktionen mit Periode 360 Grad.

Wertebereich und spezielle Funktionswerte

Die Sinusfunktion und die Kosinusfunktion können für reelle Argumente nur Werte zwischen -1 und 1 annehmen.

Verlauf des Sinus in den vier Quadranten

In den vier Quadranten ist der Verlauf der Sinusfunktion folgendermaßen:

Quadrant	Grad	Bogenmaß	Bildmenge	Monotonie	Konvexität	Punkttyp
	$0^{\circ }$	0	0			Nullstelle, Wendepunkt
1. Quadrant	$0^{\circ }<x<90^{\circ }$	$0<x<\pi /2$	positiv: $0<\sin x<1$	steigend	konkav
	$90^{\circ }$	$\pi /2$	1			Maximum
2. Quadrant	$90^{\circ }<x<180^{\circ }$	$\pi /2<x<\pi$	positiv: $0<\sin x<1$	fallend	konkav
	$180^{\circ }$	$\pi$	0			Nullstelle, Wendepunkt
3. Quadrant	$180^{\circ }<x<270^{\circ }$	$\pi <x<3\pi /2$	negativ: $-1<\sin x<0$	fallend	konvex
	$270^{\circ }$	$3\pi /2$	$-1$			Minimum
4. Quadrant	$270^{\circ }<x<360^{\circ }$	$3\pi /2<x<2\pi$	negativ: $-1<\sin x<0$	steigend	konvex

Für Argumente außerhalb dieses Bereiches erhält man den Wert des Sinus daraus, dass der Sinus periodisch mit der Periode 360° (bzw. 2π Radiant) ist, d. h. $\sin(\alpha +360^{\circ })=\sin(\alpha )$ . Außerdem gilt $\sin(\alpha +180^{\circ })=-\sin(\alpha )$ .

Verlauf des Kosinus in den vier Quadranten

Der Kosinus ist ein um 90° (bzw. π/2 Radiant) phasenverschobener Sinus, es gilt $\cos(\alpha )=\sin(\alpha +90^{\circ })$ .

In den vier Quadranten ist der Verlauf der Kosinusfunktion daher folgendermaßen:

Quadrant	Grad	Bogenmaß	Bildmenge	Monotonie	Konvexität	Punkttyp
	$0^{\circ }$	0	1			Maximum
1. Quadrant	$0^{\circ }<x<90^{\circ }$	$0<x<\pi /2$	positiv: $0<\cos x<1$	fallend	konkav
	$90^{\circ }$	$\pi /2$	0			Nullstelle, Wendepunkt
2. Quadrant	$90^{\circ }<x<180^{\circ }$	$\pi /2<x<\pi$	negativ: $-1<\cos x<0$	fallend	konvex
	$180^{\circ }$	$\pi$	$-1$			Minimum
3. Quadrant	$180^{\circ }<x<270^{\circ }$	$\pi <x<3\pi /2$	negativ: $-1<\cos x<0$	steigend	konvex
	$270^{\circ }$	$3\pi /2$	$0$			Nullstelle, Wendepunkt
4. Quadrant	$270^{\circ }<x<360^{\circ }$	$3\pi /2<x<2\pi$	positiv: $0<\cos x<1$	steigend	konkav

Für Argumente außerhalb dieses Bereiches erhält man den Wert des Koinus daraus, dass der Kosinus so wie der Sinus periodisch mit der Periode 360° (bzw. 2π Radiant) ist, d. h. $\cos(\alpha +360^{\circ })=\cos(\alpha )$ . Außerdem gilt $\cos(\alpha +180^{\circ })=-\cos(\alpha )$ .

Wichtige Funktionswerte

Eine Reihe einfach zu merkender und häufig verwendeter Werte:

$\sin(0^{\circ })=\cos(90^{\circ })={\frac {\sqrt {0}}{2}}=0$
$\sin(30^{\circ })=\cos(60^{\circ })={\frac {\sqrt {1}}{2}}={\frac {1}{2}}$
$\sin(45^{\circ })=\cos(45^{\circ })={\frac {\sqrt {2}}{2}}={\sqrt {\frac {1}{2}}}$
$\sin(60^{\circ })=\cos(30^{\circ })={\frac {\sqrt {3}}{2}}$
$\sin(90^{\circ })=\cos(0^{\circ })={\frac {\sqrt {4}}{2}}=1$

Zusammenhang zwischen Sinus und Kosinus

\sin(\alpha )=\cos \left({\frac {\pi }{2}}-\alpha \right)=\cos \left(\alpha -{\frac {\pi }{2}}\right)

\sin ^{2}\left(\alpha \right)+\cos ^{2}(\alpha )=1

(Satz des Pythagoras)

Insbesondere folgt daraus $|\sin(\alpha )|\leq 1$ und $|\cos(\alpha )|\leq 1$ . Diese Ungleichung gilt aber nur für reelle $\alpha$ ; für die über die Potenzreihe definierten komplexen Argumente können Sinus und Kosinus beliebige Werte annehmen.

\sin ^{\prime }(\alpha )=\cos(\alpha )

,

\cos ^{\prime }(\alpha )=-\sin(\alpha )

(Ableitung, siehe weiter unten)

\int \sin(\alpha )\,{\rm {d}}\alpha =-\cos(\alpha )+C

,

\int \cos(\alpha )\,{\rm {d}}\alpha =\sin(\alpha )+C

(Stammfunktion)

Zusammenhang mit den Arkusfunktionen

\sin(\arccos(x))={\sqrt {1-x^{2}}}

, das folgt aus

\sin(y)={\sqrt {1-\cos ^{2}y}}

und

y=\arccos(x)\!

.

\cos(\arcsin(x))={\sqrt {1-x^{2}}}

, das folgt aus

\cos(y)={\sqrt {1-\sin ^{2}y}}

und

y=\arcsin(x)\!

.

\sin(\arctan(x))={\frac {x}{\sqrt {1+x^{2}}}}

, das folgt aus

\sin(y)={\frac {\tan y}{\sqrt {1+\tan ^{2}y}}}

und

y=\arctan(x)\!

.

\cos(\arctan(x))={\frac {1}{\sqrt {1+x^{2}}}}

, das folgt aus

\cos(y)={\frac {1}{\sqrt {1+\tan ^{2}y}}}

und

y=\arctan(x)\!

.

Zusammenhang mit dem Skalarprodukt

Der Kosinus steht in enger Beziehung mit dem Skalarprodukt zweier Vektoren ${\vec {a}}=\left(a_{1},a_{2},\dots ,a_{n}\right)$ und ${\vec {b}}=\left(b_{1},b_{2},\dots ,b_{n}\right)$ :

{\vec {a}}\cdot {\vec {b}}=|{\vec {a}}|\cdot |{\vec {b}}|\cdot \cos \angle \left({\vec {a}},{\vec {b}}\right)={a_{1}}{b_{1}}+{a_{2}}{b_{2}}+\dots +{a_{n}}{b_{n}}

,

das Skalarprodukt ist also die Länge der Vektoren multipliziert mit dem Kosinus des eingeschlossenen Winkels. In endlichdimensionalen Räumen lässt sich diese Beziehung aus dem Kosinussatz ableiten. In abstrakten Vektorräumen mit innerem Produkt wird über diese Beziehung der Winkel zwischen Vektoren definiert.

Additionstheoreme

Aus dem Skalarprodukt lassen sich die sogenannten Additionstheoreme herleiten:

Die Vektoren ${\vec {a}}=\left(\cos \alpha ,\sin \alpha \right)$ und ${\vec {b}}_{1}=\left(\cos \beta ,\sin \beta \right)$ der Länge 1 schließen den Winkel $\alpha -\beta$ ein; mit dem Skalarprodukt folgt also

\cos \left(\alpha -\beta \right)={\vec {a}}\cdot {\vec {b}}_{1}=\cos \alpha \cos \beta +\sin \alpha \sin \beta

.

Die Vektoren ${\vec {a}}=\left(\cos \alpha ,\sin \alpha \right)$ und ${\vec {b}}_{2}=\left(\cos \beta ,-\sin \beta \right)$ der Länge 1 schließen den Winkel $\alpha +\beta$ ein; mit dem Skalarprodukt folgt also

\cos \left(\alpha +\beta \right)={\vec {a}}\cdot {\vec {b}}_{2}=\cos \alpha \cos \beta -\sin \alpha \sin \beta

.

Aus $\sin \alpha =\cos \left(\alpha -90^{\circ }\right)$ und $\sin \left(\alpha -90^{\circ }\right)=\cos \left(\alpha -180^{\circ }\right)=-\cos \alpha$ erhält man die Additionstheoreme für den Sinus:

\sin \left(\alpha +\beta \right)=\cos \left(\alpha -90^{\circ }+\beta \right)=\cos \left(\alpha -90^{\circ }\right)\cos \beta -\sin \left(\alpha -90^{\circ }\right)\sin \beta =\sin \alpha \cos \beta +\cos \alpha \sin \beta

sowie

\sin \left(\alpha -\beta \right)=\cos \left(\alpha -90^{\circ }-\beta \right)=\cos \left(\alpha -90^{\circ }\right)\cos \beta +\sin \left(\alpha -90^{\circ }\right)\sin \beta =\sin \alpha \cos \beta -\cos \alpha \sin \beta

.

Ableitung (Differentiation) von Sinus und Kosinus

Nachfolgend wird eine geometrische Berechnung der Ableitung der Sinusfunktion dargestellt. Eine exakte Berechnung mit Methoden der Analysis ist nicht möglich, da Sinus und Kosinus bisher nur gemoetrisch und nicht analytisch definiert sind.

Der Nachweis wird mit Hilfe des Einheitskreises erbracht, wobei der Winkel zweckmäßigerweise im Bogenmaß angegeben wird.

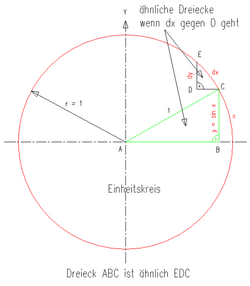
Aus der Skizze kann man folgende Zusammenhänge erkennen.

x ist das Bogenmaß zum Sinuswert. Im Einheitskreis ist

y\ =\sin(x)

Ändert sich der Bogen x um das Maß dx, so ergibt sich auch das Maß dy. Denkt man sich dx gegen Null gehend, so ergeben sich zwei ähnliche Dreiecke ABC und EDC. Setzt man diese ins Verhältnis so erhält man die Verhältnisgleichung

{\frac {dy}{dx}}={\frac {\overline {AB}}{1}}

Da die Strecke

{\overline {AB}}=\cos(x)

ist und

y^{\prime }={\frac {dy}{dx}}

die Ableitung ist, ergibt sich als Lösung

y^{\prime }=\cos(x)

.

Aus $\cos(x)=\sin \left({\frac {\pi }{2}}-x\right)$ und der Kettenregel erhält man die Ableitung des Kosinus:

\cos ^{\prime }(x)=-\sin(x)

und daraus die zweite Ableitung des Sinus:

\sin ^{\prime \prime }(x)=-\sin(x)

.

Die dritte Ableitung ist daher

\sin ^{\prime \prime \prime }(x)=-\cos(x)

.

und die vierte Ableitung ist wieder die Sinusfunktion selbst:

\sin ^{\prime \prime \prime \prime }(x)=\sin(x)

.

In weiterer Folge erhält man daraus für die $4n+k$ -te Ableitung des Sinus

\sin ^{(4n+k)}(x)=\left\{{\begin{matrix}\sin(x)&{\mbox{wenn }}k=0\\\cos(x)&{\mbox{wenn }}k=1\\-\sin(x)&{\mbox{wenn }}k=2\\-\cos(x)&{\mbox{wenn }}k=3\end{matrix}}\right.

und für die $4n+k$ -te Ableitung des Kosinus

\cos ^{(4n+k)}(x)=\left\{{\begin{matrix}\cos(x)&{\mbox{wenn }}k=0\\-\sin(x)&{\mbox{wenn }}k=1\\-\cos(x)&{\mbox{wenn }}k=2\\\sin(x)&{\mbox{wenn }}k=3\end{matrix}}\right.

Diese Beziehung gilt nur, wenn $x$ im Bogenmaß angegeben wird. Wird der Winkel $\alpha$ in Grad gemessen, so kommt nach der Kettenregel bei jeder Ableitung ein Faktor ${\frac {\pi }{180}}$ dazu, also beispielsweise $\sin ^{\prime }(\alpha )={\frac {\pi }{180}}\cos(\alpha )$ . Um diese störenden Faktoren zu vermeiden, wird in der Analysis der Winkel ausschließlich im Bogenmaß angegeben; die Angabe von Winkel in Grad ist allerdings anschaulicher und daher bei geometrischen Überlegungen zweckmäßiger.

Analytische Definition

Obige Definitionen des Sinus und des Kosinus beinhalten geometrische Überlegungen. Sinus und Kosinus spielen auch eine wichtige Rolle in der Analysis, allerdings sind geometrischen Definitionen für die Analysis nicht zweckmäßig, daher wird eine eine analytische Defintion benötigt. Die analytische Definition erlaubt zusätzlich die Erweiterung auf komplexe Argumente. Sinus und Kosinus als komplexwertige Funktion aufgefasst sind holomorph und surjektiv.

Reihenentwicklung des Sinus und des Kosinus

Mit Hilfe der aus geometrischen Überlegungen berechneten Ableitung des Sinus gilt für die $4n+k$ -te Ableitung an der Stelle 0

\sin ^{(4n+k)}(0)=\left\{{\begin{matrix}0&{\mbox{wenn }}k=0\\1&{\mbox{wenn }}k=1\\0&{\mbox{wenn }}k=2\\-1&{\mbox{wenn }}k=3\end{matrix}}\right.

Daraus ergibt sich folgende Taylorreihenentwicklung um x=0:

\sin(x)=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n+1}}{(2n+1)!}}={\frac {x}{1!}}-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\ldots =x-{\frac {x^{3}}{6}}+{\frac {x^{5}}{120}}-\ldots

Für die aus geometrischen Überlegungen berechneten Ableitung des Kosinus gilt für die $4n+k$ -te Ableitung an der Stelle 0

\cos ^{(4n+k)}(0)=\left\{{\begin{matrix}1&{\mbox{wenn }}k=0\\0&{\mbox{wenn }}k=1\\-1&{\mbox{wenn }}k=2\\0&{\mbox{wenn }}k=3\end{matrix}}\right.

Daraus ergibt sich folgende Taylorreihenentwicklung um x=0:

$\cos(x)=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n}}{(2n)!}}=1-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-...$

Mit dem Quotientenkriterium lässt sich zeigen, dass diese Potenzreihen für jede komplexe Zahl x absolut und in jeder beschränkten Teilmenge der komplexen Zahlen gleichmäßig konvergieren. Diese Reihen verallgemeinern also die Definition des Sinus und des Kosinus von reellen auf komplexe Argumente. In der Analysis werden die Sinusfunktion und die Kosinusfunktion üblicherweise mittels dieser Reihenentwicklung definiert. Auch $\pi$ wird in der Analysis üblicherweise nicht geometrisch, sondern über diese Reihe und die Beziehung $\cos \left({\frac {\pi }{2}}\right)=0$ als das Doppelte der kleinsten positiven Nullstelle der Kosinusfunktion defniert.

Für kleine Werte zeigen diese Reihen ein sehr gutes Konvergenzverhalten. Zur numerischen Berechnung kann man daher die Periodizität und Symmetrie der Funktionen ausnutzen und den x-Wert bis auf den Bereich -π/4 bis π/4 reduzieren (siehe Reduktionsformel). Danach sind für eine geforderte Genauigkeit nur noch wenige Glieder der Reihe zu berechnen. Das Taylorpolynom der Kosinusfunktion bis zur vierten Potenz z.B. hat im Intervall [-π/4, π/4] einen relativen Fehler von unter 0,05%. Im Artikel Taylor-Formel sind einige dieser so genannten Taylorpolynome grafisch dargestellt und eine Näherungsformel mit Genauigkeitsangabe angegeben. Zu beachten ist allerdings, dass die Teilsummen der Taylorpolynome nicht die bestmögliche numerische Approximation darstellen; im "Handbook of Mathematical Functions" von Abrahmovitz und Stegun finden sich Näherungspolynome mit noch kleinerem Approximationsfehler.

Definition mit Hilfe der Exponentialfunktion

Die trigonometrischen Funktionen können auch mit Hilfe der Exponentialfunktion definiert werden. Dieser Ansatz führt zum einen Sinus und Kosinus auf nur eine Reihe zurück, und ist aus der Eulerformel

e^{i\varphi }=\cos \left(\varphi \right)+i\sin \left(\varphi \right)

.

motiviert. Für eine reelle Zahl $\varphi$ ist also $\cos \left(\varphi \right)$ der Realteil von $e^{i\varphi }$ und $\sin \left(\varphi \right)$ der Imaginärteil von $e^{i\varphi }$ .

Für beliebige komplexe Zahlen $z$ definiert man dann

\sin z={1 \over 2i}\left(e^{iz}-e^{-iz}\right)

und

\cos z={1 \over 2}\left(e^{iz}+e^{-iz}\right)

Selbstverständlich kann man auch den Sinus wie oben als Taylorreihe definieren und dann die Übereinstimmung mit dieser Definition zeigen.

Ausgehend von dieser Definition lassen sich sehr leicht die Eigenschaften des Sinus und die Additionstheoreme des Sinus und Kosinus nachweisen.

Anwendungen

Geometrische Anwendungen

Mit der Definition des Sinus können auch im nicht rechtwinkligen Dreieck Größen, speziell die Höhen, berechnet werden; ein Beispiel ist die Berechnung von $h_{c}$ im Dreieck DBC bei gegebener Länge $a$ und Winkel β:

${\frac {h_{c}}{a}}=\sin(\beta )$

$h_{c}=a\cdot \sin(\beta )$

$h_{c}=5,\!4~{\rm {[LE]}}\cdot \sin(44^{\circ })=3,\!751~{\rm {[LE]}}$

Andere wichtige Anwendungen sind der Sinussatz und der Kosinussatz.

Fourierreihen

Im Hilbertraum $L^{2}[-\pi ,\pi ]\!$ der auf dem Intervall $[-\pi ,\pi ]\!$ bezüglich des Lebesgue-Maßes quadratisch integrierbaren Funktionen bilden die Funktionen

1,\cos nx,\sin nx\quad n=1,2,\dots

ein vollständiges Orthogonalsystem, das sogenannte trigonometrische System. Daher lassen sich alle Funktionen $f\in L^{2}[-\pi ,\pi ]$ als Fourierreihe

S_{n}(x)={\frac {a_{0}}{2}}+\sum _{k=1}^{n}(a_{k}\cos nx+b_{k}\sin nx)

darstellen, wobei die Funktionenfolge $S_{n}(x)\!$ in der $L^{2}$ -Norm gegen $f(x)\!$ konvergiert.

Physikalische Anwendungen

In der Physik werden Sinus- und Kosinusfunktion zur Beschreibung von Schwingungen verwendet. Insbesondere lassen sich durch die oben erwähnten Fourierreihen beliebige Signale als Summe von Sinus- und Kosinusfunktionen darstellen, siehe Fourieranalyse.

Herkunft des Namens

Die Bezeichnung "Sinus" leitet sich von dem lateinischen "sinus" ab, was soviel heißt wie "Bogen" oder "Busen". Das Wort ist mit "jiva" aus dem Sanskrit verwandt, wo es etwa "Bogensehne" bedeutet. Im Arabischen entwickelte sich das Wort zu "jiba": "Tasche" oder "Kleiderfalte". "Kosinus" bedeutet "Sinus des Komplementärwinkels".

Weitere Bedeutung

Kosinus ist auch eine Comicfigur einer deutschen Computerzeitschrift.
COS, das Krypto-Betriebssystem war einer der größten Fakes in der Mac-Geschichte

SINUS ist auch das Akronym für die Weiterbildungsinitiative zur Steigerung der Effizienz des mathematisch-naturwissenschaftlichen Unterrichts [URL: http://blk.mat.uni-bayreuth.de/indexblk.html bzw. http://www.sinus-transfer.de/]

Siehe auch

Links

Java Applet "Dreieck und Sinussatz" zur Veranschaulichung [URL: http://www.mathe-online.at/mathint/trig/applet_b_dreieck.html]
Näherungspolynome aus Abramowitz and Stegun