MCS algorithm

Figure 1: MCS algorithm (without local search) applied to the two-dimensional Rosenbrock function. The global minimum $f_{min}=0$ is located at $(x,y)=(1,1)$. MCS identifies a position with $f\approx 0.002$ within 21 function evaluations.

Multilevel Coordinate Search (MCS) is an efficient algorithm for bound constrained global optimization using function values only.

To do so, the n-dimensional search space is represented by a set of non-intersecting hypercubes (boxes). The boxes are then iteratively split along an axis plane according to the value of the function at a representative point of the box (and its neighbours) and the box's size. These two splitting criteria combine to form a global search by splitting large boxes and a local search by splitting areas for which the function value is good.

Additionally, a local search combining a (multi-dimensional) quadratic interpolant of the function and line searches can be used to augment performance of the algorithm (MCS with local search). In this case the plain MCS is used to provide both starting points and search directions. The information provided by local searches (namely local minima of the objective function) is then fed back to the optimizer and influences the splitting criteria, resulting in reduced sample clustering around local minima.

Simplified workflow

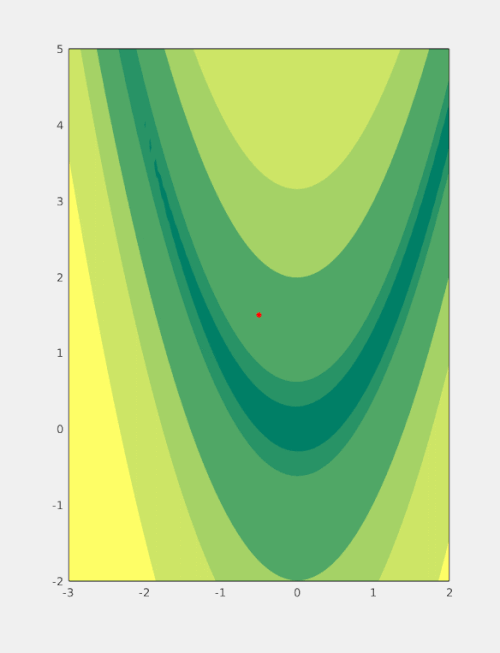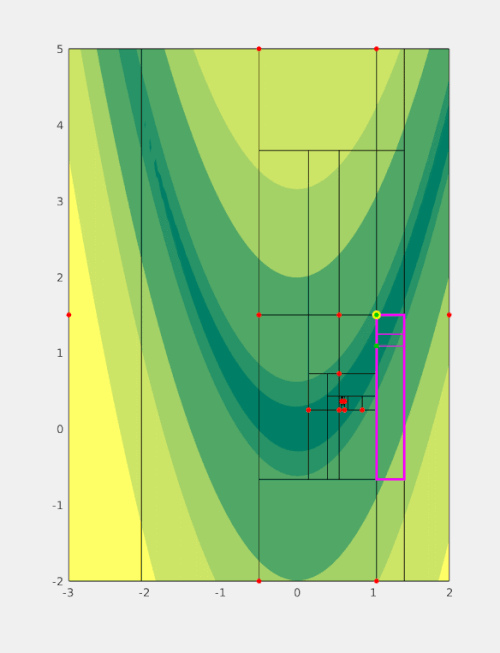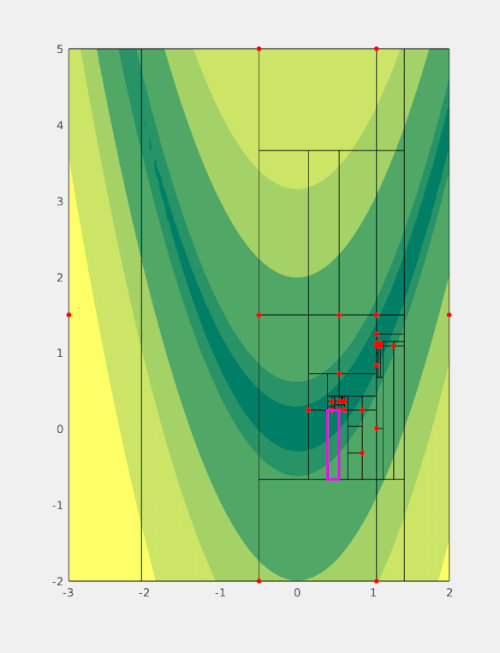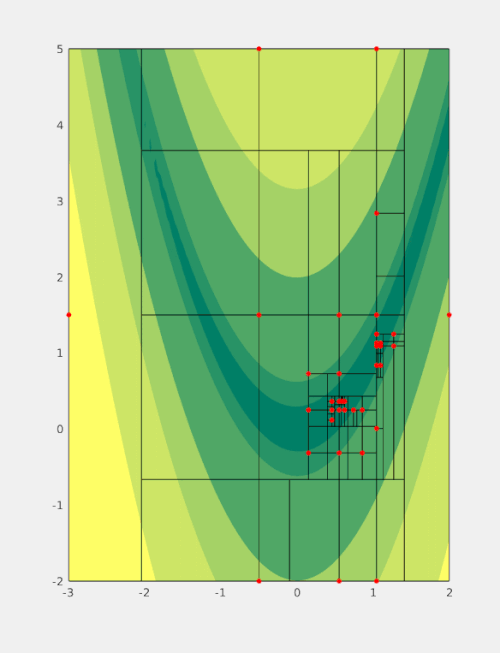
The basic workflow is presented in figure 1. Generally, each step can be characterized by three stages:

1. Identify a potential candidate for splitting (magenta, thick).
2. Identify the optimal splitting direction and the expected optimal position of splitting points (green).
3. Evaluate the objective function at splitting points not considered previously. Generate new boxes (magenta, thin) based on the values of the objective function at splitting (green) points.

At every step at least one splitting point (yellow) is a known function sample (red) hence the objective is never evaluated there again.

Convergence

The algorithm is guaranteed to converge to the global minimum in the long run (i.e. when the number of function evaluations and the search depth are arbitrarily large) if the objective function is continuous in the neighbourhood of the global minimizer. This follows from the fact that any box will become arbitrarily small eventually, hence the spacing between samples tends to zero as the number of function evaluations tends to infinity.

Recursive implementation

MCS was designed to be implemented in an efficient recursive way with the aid of trees. With this approach the amount of memory required is independent of problem dimensionality since the sampling points are not stored explicitly. Instead, just a single coordinate of each sample is saved and the remaining coordinates can be recovered by tracing the history of a box back to the root (initial box). This method was suggested by the authors and used in their original implementation.

When implemented carefully this also allows for avoiding repeated function evaluations. More precisely, if a sampling point is placed along the boundary of two adjacent boxes then this information can often be extracted through backtracing the point's history for a small number of steps. Consequently, new subboxes can be generated without evaluating the (potentially expensive) objective function. This scenario is visualised in figure 1 whenever a green (but not yellow) and a red point coincide e.g. when the box with corners around $(-0.5,0.5)$ and $(1.0,3.5)$ is split.

External links

• Homepage of the algorithm
• Performance of the algorithm relative to others