Tango tree

A Tango tree is an online binary search tree that is $O{\Bigl (}\lg \lg(n){\Bigr )}$ -competitive.

Tango Trees were invented by Erik D. Demaine, Dion Harmon, John Iacono, and Mihai Pătraşcu in 2004.

They were designed to surpass the usual $O{\Bigl (}\lg \lg(n){\Bigr )}$ binary search tree cost of operations. They perform basic operations such as searches in $O{\Bigl (}\lg \lg(n){\Bigr )}$ time. This optimization is achieved dynamically by adjusting the search tree structure as a result of all searches. They are similar in their dynamic behaviour to other types of structure like a Splay tree. However, the search speed is considerably improved.

They achieve this by a combination of augmentation of attributes in the data structure, a more elaborated algorithm and the use of other type of trees for some of its structure.

The main idea behind this data structure is to extract from the original tree a number of virtual smaller subtrees all with a normal O(lg number of subtree elements) cost of access. These subtrees are dynamically balanced to offer the usual $O{\Bigl (}\lg \lg(n){\Bigr )}$ performance for data retrieval. Via this classic divide and conquer approach, once the original tree has been adjusted to include a collection of these subtrees, it is possible to greatly improve the cost of access of these subtrees. Both the Tango tree and these subtrees are a type of Self-balancing binary search tree.

Advantages

Tango Trees offer fast retrieval speed for online data. Online structures deal with operations that are not known in advance before the data structure is created.

Outstanding search performance for a Tango tree relies on the fact that accessing nodes constantly update the structure of the search trees. That way the searches are rerouted to searches in much shallower balanced trees.

Obviously significantly higher access time constitutes an advantage for nearly all practical applications that offer searches as a use case. Dictionary searches like telephone directory search would be just one of the possible an examples.

Disadvantages

The Tango tree focuses on data searches on static data structures, rather than on deletions or insertions, so they might not be appropriate in any situation.

The Tango tree uses augmentation, meaning storing more data in a node that a plain binary search tree. Tango trees use $O{\Bigl (}\lg \lg(n){\Bigr )}$ bits. Although that is not a significant increase, it results in a bigger memory footprint.

It is a complex algorithm to implement, since it makes use of other algorithms like Red-Black Tree and balancing operations.

Tango trees change n when they are accessed in a 'read-only' manner (i.e. by find operations). This complicates the use of Tango trees in a multi-threaded environment.

Operations

Here are some elements necessary to understand why the Tango Tree achieve such an amazing performance $O{\Bigl (}\lg \lg(n){\Bigr )}$ . We should start with some definitions and go through some great sources of literature which have been done in this field.

Wilber's 1st Lower Bound [Wil89] notes that fix an arbitrary static lower bound tree P with no relation to the actual BST T, but over the same keys. In the application that we consider, P is a perfect binary tree. For each node y in P, we label each access X1 L if key X1 is in y's left subtree in P, R if key X1 is in y's right subtree in P, or leave it blank if otherwise. For each y, we count the number of interleaves (the number of alterations) between accesses to the left and right subtrees: interleave(y)= ♯ of alternations L ↔ R.

Wilber's 1st Lower Bound [Wil89] states that the total number of interleaves is a lower bound for all BST data structures serving the access sequence x. It is important to note that the lower bound tree P must remain static. Proof.(sketch) We define the transition point of y in P to be the highest node z in the BST T such that the root-to-z path in T includes a node from the left and right subtrees if y in P. Observe that the transition point is well defined, and does not change until we touch z. In addition, the transition point is unique for every node y.

Search

High level To search for a node x in a Tango tree, we search for the element in the collection of Auxiliary Trees like in an ordinary binary search tree, then adjust the corresponding affected Auxiliary Trees in the Tango Tree. This will be an ideal structure that will give us this unprecedented search speed.

The reasons why such a structure $O{\Bigl (}\lg \lg(n){\Bigr )}$ is explained in the Analysis

That could be accomplished by updating the Reference Tree P after every search and recreating the Tango tree. We could realize this structure by recalculating the collection of preferred paths, re-creating the Auxiliary trees and append the new Auxiliary Trees as the leaf nodes of the previous Tango Tree.

Obviously this would be very expensive and nonperformance.

The goal is to find performance way to update the Tango Tree directly without ever using the initial Reference Tree. That can be accomplished and we are going to explain how.

Tango Tree Life Cycle

The main phases are: First create the reference tree and insert the desired data in it. Update the attributes of depth for each node After this phase the data and the vale of the depth of the nodes will remain unchanged. The Reference tree can be any balanced tree that is augmented with the depth of each node in the tree. Let's call that field d for further reference. Secondly we will perform some warm-up searches with the goal to create a decent distribution of Preferred Paths in the Reference Tree. Remember there is no Tango tree and all this is done on line. This means that performance is not critical at this point.

After this begins the phase of collecting and descendantly sorting the preferred Paths by Length. Out of each Preferred Path we create a new Auxiliary Tree which is just an ordinary RedBlack Tree where the nodes inherit the value of field d. That value will stay unchanged forever because it stays with the node even if the node is moved in the trees.

add another section after main operations called Tango Tree Augmentation:

For each of these Auxiliary Tree we also introduce 3 new fields:

iSRoot that will be false for all nodes except for the root.

maxD that is the Maximum value of d for all the children of the node

minD that is the Minimum value of d for all the children of the node

iSRoot, maxD and minD will change in time when nodes are moved around in the structure.

Again there is no Tango Tree at this point.

Analysis

Lemma 1

The running time of an access xi is $O{\Bigl (}(k+1)(1+lglg(n)){\Bigr )}$ , where k is the number of nodes whose preferred child changes during access xi.

Lemma 2

The number of nodes whose preferred child changes from left to right or from right to left during an access xi is equal to the interleave bound ${\Bigl (}IBi(X{\Bigr )}$ of access xi.

Theorem 1

The running time of the Tango BST on an sequence X of m accesses over the universe ${1,2,...,n}.$ is $O{\Bigl (}(OPT(X)+n)(1+lglg(n)){\Bigr )}$ where $OPT{\Bigl (}X{\Bigr )}$ is the cost of the offline optimal BST servicing X.

Corollary 1.1

When m = (n), the running time of the Tango BST is

$O{\Bigl (}OPT(X)(1+lglg(n)){\Bigr )}$

Fix an arbitrary static lower bound tree P with no relation to the actual BST T, but over the same keys. In the application that we consider, P is a perfect binary tree. For each node y in P, we label each access X1 L if key X1 is in y's left subtree in P, R if key X1 is in y's right subtree in P, or leave it blank if otherwise. For each y, we count the number of interleaves (the number of alterations) between accesses to the left and right subtrees: interleave(y)= ♯ of alternations L ↔ R

-BST model

-Comparativeness def
-Splay configured

- PP ↔ TANGO connection

- If no reconfiguring cost how much

- How do you do reconfiguring in kloglog u

Back to BST model

- Given sequence of accesses

X=<X1,X2,...,Xm>

What would it mean to say that some BST execute this sequence optimally that is best possible
- If we are allowed to look at X → D off-line BSTs
- If not → on-line (dynamic) BST

Question: Is the dy-BST that executes X as well as best off-line BST for X
Relationship (or ? there of) to entropy y

Why does the fact that splay trees met entropy bound does not answer the above question?

SET UP:
Assume over $[n]={1,2,....n}$
Access sequence $X=<X1,X2,...Xm>$ €[n]^m
- $O{\Bigl (}\lg \lg(n){\Bigr )}$ must process the sequence in order
MODEL: - Search from the root to X_i and then before some arbitrary num of rotation

COST: num nodes in search path + num of rotations

DEF: OPT(x): smallest cost over all (off-line) BST i.e length of the shortest sequence that executes X
COMPETITIVENESS
BST runs X in K.OPT(X)→K competitive
if K cost → DYNAMICALUU

- Splay configured to be OPTIMA BST

But in fact not known if such BST even exists.
What is comparativeness of BALANCES STATIC BST?

Trivially (m logn)

- one of the most important or at least most frustrating O in DS_i:

Is there O(₁) competitive BST

- until recently only trivially O(log) Comparativeness (obtained by balances BST) was best known
Trivial upper bound for balanced BST was obtained lower bound Ω(m).
Need better LB.

LOWER BOUND
Trivial lower bound Ω(m)

Wilber interleave bound W2

Defined with respect to arbitrary (but fixed) tree P. take P→ perfect BST

left region $L(y)=y+itsleftsubtree$
right region $R(y)=itsrightsubtree$

the amount of interleaving through y: $I(y)$

$L(7)={7,6}$
$R(7)={9,8}$

e.g.
X=<3,1,4,1,5,9,2,6,5,3,5,8,9,7,3, 2,3,8,4,6,L7>
x⁷=<9,6,8,9,78,6,7>
I(y)=5

INTERLEAVE BOUND: W2

File:Diagram05.jpg

for any access tag X and any ref tree P examples
EXAMPLES SCANNING

File:Diagram07.jpg

→ OPT(X)=Ω(m)
achievable by SPLAY

In fact: think of what DYNAMIC FINGER says
EXAMPLE RANDOM X

|B(randomX)=Ω(mlog)
that is highest W2 can give
Ω(mlog)→ worst case

IDEA FOR TANGO (good BST)
Simulate interleave bound
DIFFERENT VIEW OF INTERLEAVE BOUND
PREFERRED PATH
node if: its preferred child indicates
if L(y) or R(y) contains the latest accessed element accessed by element in X
[[ Image:1 Reference tree after inserting all the elements and before any searches, d is the depth in tree, Md is the Max depth of a node considering all it's subchildren.JPG| frame | center | sizepx |Reference Tree after inserting all the elements and before any searches. d is the depth in tree. Md is the Max depth of a node considering all it's subchildren]]

Reference Tree after first search for element 17

Reference Tree after first 2 searches for 17 and 7

Reference Tree after performing searches for 17,7,1,18,23,31,27,13,9

preferred paths after accesses:
X=<7,1,18,23,31,2713,9...>
-since reference tree is balanced high of Ǝ per. path O(logn)

Back to interleave
|B(X)=total ♯ times
the preferred paths changes as we execute X

IDEA FOR BST (tango)
Simulate IB(x)
Tango: after every access to element in X, preferred paths, in P are redefined.
WANT TANGO after EVERY ACCESS
to look as follows

top AUXILIARY TBE preferred path at balanced BST

second level Preferred Paths

third level etc

Reference Tree P with Preferred Paths marked in red after performing all warm-up searches for elements 17,7,1,18,23,31,27,13,9,20 searches

NOTICE: because preferred paths are PATHS, all the children subpaths form consecutive keys in[n]
thus the subtree hang in different places on top path

height of every path representation in TANGO is $O{\Bigl (}\lg \lg(n){\Bigr )}$ since P has O(log) vertices

tango of previous example

7 Second formed Auxiliary Tree formed from a Preferred Path from the previously searched Reference Tree.

Last Auxiliary Tree to be added to the Tango Tree, note that nodes that are not part of a preferred path become one node Auxiliary Trees.

9 Tango Tree based on previous Reference Tree where the first 2 Auxiliary Trees were added.

Tango Tree generated from the reference Tree P after the last warm-up search for for element 20, Nodes in pink are roots of Auxiliary Trees.

IMAGINING that after every access the TANGO looks the way we want (that is as defined above) and that we get that MAGICALLY FOR TREE. So we are not concerned how we get from Tango T_i to Tango T_i+1 after accessing X_i+1.

Given that for tree

How much would just accesses that is searches, of X COST

X=<X₁,X₂,...X_i,...X_m> how much is access to X_i in T_i O(K_i.loglogn)

number of times preferred child changes while searching for X_i

thus access to the whole X costs

File:Diagram03.jpg

cost searches ≤ O(IB_(x).loglogn)≤O(opt(x),logn) given transformation for tree

REST OF CLASS

System accessing Xi how do we transform T_i to T_i+1
spending O(Klglogn) time

(that is same time as accessing Xi)

We would then need following operations on Auxiliary Trees

search
cutting Aux Tree in 2

1 containing all elements at dept≤ d in P

2-containing all elements at dept > d in P

joining 2 Aux Trees that store disjoint paths when the bottom of one

Each preferred path as Auxiliary Tree -> RB tree

3 additional info in every node of AUX Tree

1. own depth in P
2. max depth in its subtree
3. node is marked if root of AUX Tree

join + cut can be achieved by standard RB tree operation

- split at x

- concatenate two RB trees

- HOW TO DO CUT IN TANGO

Reference Tree after inserting all the elements and before any searches. d is the depth in tree. Md is the Max depth of a node considering all it's subchildren

Remember the Reference Tree after warm-up search for 20 looked like this

If after that we would do a search for 30 it would have looked like this, where the path 16,24,20,22 and 23 becoming 16 , 24, 28, 30 therefore loosing 20, 22 and 23

Tango Tree after search for 20 with the Auxiliary tree corresponding

Tango Tree after search for 20 with the Auxiliary tree corresponding to the preferred path that will change after searching for 30 and cut points l, l, l prime and r prime marked

- You can find l in AUX by going to left child as long as its subtree contains an element of greater depth then l

-similarly you can find r

l' = predecessor of l
r'= successor of r

CUT

Implementation Tango Cut using RedBlack Split

Tango Join Algorithm as a Sequence of Tree Split Un-mark and Concatenate RP Operations

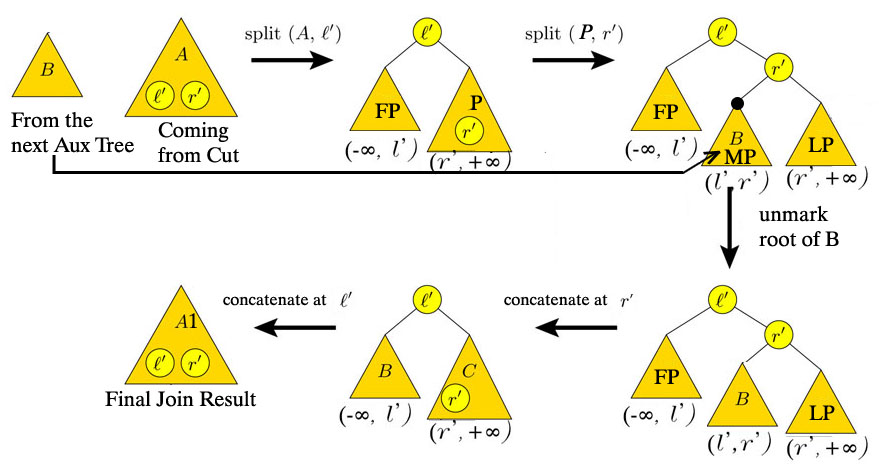
FINISH OF BY

- cut of D (by concatenating its root)

- merge c,l,r,& E all done in $O{\Bigl (}\lg \lg(n){\Bigr )}$ time

Bibliography

Erik D. Demaine, Dion Harmon, John Iacono and Mihai Pătraşcu, Dynamic optimality - almost [competitive online binary search tree], In Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, pages 484–490, Rome, Italy, October 2004, http://ieeexplore.ieee.org/xpl/mostRecentIssue.jsp?punumber=9430

Allen, Brian; and Munro, Ian (1978), "Self-organizing search trees", Journal of the ACM 25 (4): 526–535, doi:10.1145/322092.322094
Knuth, Donald. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Page 478 of section 6.2.3.

References

External links

Dynamic Optimality-Almost